Dr. Yong Liang (Postdoctoral researcher), Joel Given (PhD student), and Prof. Kenichi Soga recently published a paper in Computer Methods in Applied Mechanics and Engineering, entitled “The imposition of nonconforming Neumann boundary condition in the material point method without boundary representation” (https://doi.org/10.1016/j.cma.2022.115785).
The Material Point Method (MPM) is a hybrid Eulerian-Lagrangian numerical method. As a result, nonconforming boundary conditions are common. Previous MPM variations all rely on boundary reconstruction procedures to impose any nonconforming traction (i.e., Neumann) boundary conditions. In this work, the Virtual Stress Boundary (VSB) method is proposed as an approach to impose nonconforming traction (i.e., Neumann) boundary conditions without explicitly reconstructing the boundary position. Instead, a combined particle- and cell-wise quadrature scheme is employed to impose nonconforming traction boundary conditions. This means lower computational cost compared to many existing approaches to impose traction boundary conditions.
A variety of numerical examples are included in the paper to demonstrate the capability of the proposed VSB method. Two of these numerical examples are summarized below:
-
The spatial convergence of the VSB method is quantified for a thick-walled cylinder problem. The stress and displacement contours improve with mesh refinement (Fig. 1). Note, the stress and displacement errors converge at approximately linear and quadratic rates, respectively (Fig. 2). These convergence rates match the expected rates for linear shape functions.
-
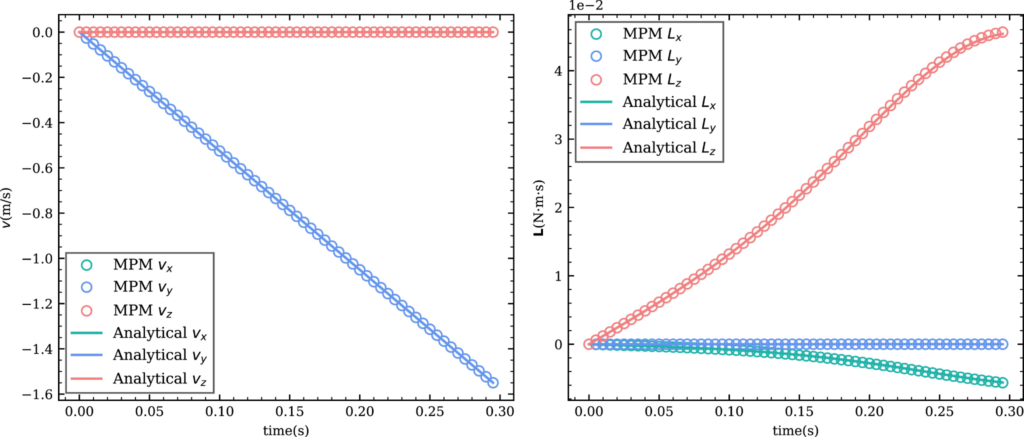
The VSB approach is particularly useful for imposing pressure boundary conditions such as hydrostatic pressure. The rotation of a complex dragon (Fig. 3) depends on the difference in density between the fluid and solid. The simulation results are aligned with analytic values (Fig. 4). Thus, even for a complex 3D body, the proposed VSB method allows for correctly imposing hydrostatic pressure without explicit boundary representation.
Fig. 1: Stress and displacement contours for the thick-walled cylinder problem during mesh refinement.
Fig. 2: Spatial convergence of stress and displacement errors for the thick-walled cylinder problem during mesh refinement.
Fig. 3: Postures of a submerged dragon model (with unequal material density) at different times.
Fig. 4: The evolution of the average velocity and the total angular momentum of the submerged dragon model (with unequal material density) as it rotates compared to analytic solution.